2023-01-03

漢字データベースを使って漢字ベン図を作問する

プログラミング漢字

漢字ベン図は、QuizKnockがやっていた漢字クイズです。条件が3つ与えられるので、複数の条件に当てはまる漢字を答えていきます。

www.youtube.com

この記事では、漢字情報データベース Mojidata を活用して、漢字ベン図を作問してみようと思います。

github.com

MojidataはSQLiteというデータベースエンジンで使うことができるデータベースになっていて、情報をSQLで取得することができます。

データベースを使う準備

Mojidataを使うには、Node.jsとSQLiteをインストールしてあると楽です。

その後、ターミナルで次のコマンドを実行して、moji.dbをダウンロードし、sqlite3を起動してください。

# 作業用のディレクトリを作る
mkdir kanji-venn
# カレントディレクトリを変更する
cd kanji-venn
# npm パッケージの初期化（node_modulesを作業用ディレクトリに作成するため）
npm init -y
# mojidataパッケージのインストール
npm install @mandel59/mojidata
# SQLiteの起動
sqlite3 node_modules/@mandel59/mojidata/dist/moji.db

SQLiteが起動すると、次のようなプロンプトが表示されます。

SQLite version 3.40.0 2022-11-16 12:10:08
Enter ".help" for usage hints.
sqlite>

個人的にはSQLiteはCLIからだと少し使いづらいと思うので、普段は自作のErqというツールを使っています。これは補完機能が使え、SQLより簡単に書けるErqクエリ言語を使って情報を取得できます。開発途中で、マニュアル等はないのですが、Erqを使ってみたい場合は、こちらもnpmでインストールして使うことができます。次のコマンドでErqをインストールします。

# Erqのインストール
npm install github:mandel59/erq
# Erqの起動
npx erq node_modules/@mandel59/mojidata/dist/moji.db

Erqを起動すると、次のようなプロンプトが表示されます。

Connected to node_modules/@mandel59/mojidata/dist/moji.db
erq>

他にDuckDBを使って読み込む方法や、GUIのツールを使う方法もあります。

漢字情報を取得してみる

作問するにあたって、漢字の次のような情報が取得したいです。

常用漢字の一覧
漢字の読み
漢字の総画数
漢字の部首
漢字の構造

常用漢字の一覧と読みは、常用漢字表のデータを格納した joyo テーブルに保存されています。また、総画数はMJ文字情報一覧のデータを格納した mji テーブルから、部首は mji_rsindex テーブルから、漢字の構造は ids テーブルから、それぞれ取得できます。

erq> joyo limit 10;;
select * from joyo limit 10
["漢字","音訓","例","備考"]
["亜","ア","[\"亜流\",\"亜麻\",\"亜熱帯\"]",""]
["哀","アイ","[\"哀愁\",\"哀願\",\"悲哀\"]",""]
["哀","あわれ","[\"哀れ\",\"哀れな話\",\"哀れがる\"]",""]
["哀","あわれむ","[\"哀れむ\",\"哀れみ\"]",""]
["挨","アイ","[\"挨拶\"]",""]
["愛","アイ","[\"愛情\",\"愛読\",\"恋愛\"]","愛媛（えひめ）県"]
["曖","アイ","[\"曖昧\"]",""]
["悪","アク","[\"悪事\",\"悪意\",\"醜悪\"]",""]
["悪","オ","[\"悪寒\",\"好悪\",\"憎悪\"]",""]
["悪","わるい","[\"悪い\",\"悪さ\",\"悪者\"]",""]
10 rows (0.011s)

読み情報ビュー kanji_reading を定義して、必要な情報だけを使いやすくします。

erq> view temp.kanji_reading = joyo {k: 漢字, r: 音訓};;
create view `temp`.kanji_reading as with kanji_reading as (select 漢字 as k, 音訓 as r from joyo) select * from kanji_reading
ok (0.002s)
erq> kanji_reading limit 10;;
select * from kanji_reading limit 10
["k","r"]
["一","ひと"]
["一","ひとつ"]
["一","イチ"]
["一","イツ"]
["丁","チョウ"]
["丁","テイ"]
["七","なな"]
["七","ななつ"]
["七","なの"]
["七","シチ"]
10 rows (0.000s)

総画数と部首、構造を取得するビューも定義します。

総画数情報ビュー kanji_strokes の定義

erq> view temp.kanji_strokes = mji[漢字施策='常用漢字']{k: 実装したUCS, s: 総画数};;
create view `temp`.kanji_strokes as with kanji_strokes as (select 実装したUCS as k, 総画数 as s from mji where (漢字施策 = '常用漢字')) select * from kanji_strokes
ok (0.000s)
erq> kanji_strokes limit 10;;
select * from kanji_strokes limit 10
["k","s"]
["一",1]
["丁",2]
["七",2]
["万",3]
["丈",3]
["三",3]
["上",3]
["下",3]
["不",4]
["与",3]
10 rows (0.001s)

部首情報ビュー kanji_radical の定義

erq> view temp.kanji_radical = mji[漢字施策='常用漢字'] -:MJ文字図形名:> mji_rsindex -:部首:> radicals {k: 対応するUCS, rad: 部首漢字};;
create view `temp`.kanji_radical as with kanji_radical as (select 対応するUCS as k, 部首漢字 as rad from mji join mji_rsindex on mji.MJ文字図形名 = mji_rsindex.MJ文字図形名 join radicals on mji_rsindex.部首 = radicals.部首 where (漢字施策 = '常用漢字')) select * from kanji_radical
ok (0.000s)
erq> kanji_radical limit 10;;
select * from kanji_radical limit 10
["k","rad"]
["一","一"]
["丁","一"]
["七","一"]
["万","一"]
["丈","一"]
["三","一"]
["上","一"]
["下","一"]
["不","一"]
["与","一"]
10 rows (0.001s)

構造情報ビュー kanji_ids の定義

erq> view temp.kanji_ids = ids[UCS in joyo{漢字}]{k: UCS, ids: IDS} distinct;;
create view `temp`.kanji_ids as with kanji_ids as (select distinct UCS as k, IDS as ids from ids where (UCS in (select 漢字 from joyo))) select * from kanji_ids
ok (0.000s)
erq> kanji_ids limit 10;;
select * from kanji_ids limit 10
["k","ids"]
["一","一"]
["丁","⿱一亅"]
["七","〾⿻乚一"]
["万","⿸丆𠃌"]
["丈","⿻𠂇乀"]
["三","三"]
["上","⿱⺊一"]
["下","⿱一卜"]
["不","⿸丆⿰丨丶"]
["不","⿻丆卜"]
10 rows (0.003s)

クイズを作問する

ここまでできれば、あとは、条件に当てはまる漢字を取得するクエリを作るだけです。先の動画の例題で言えば、「さんずい」「9画」「「せ」から始まる」といった条件は、漢字をxとすれば、SQLとErqではそれぞれ次のように表現できます。

さんずい
- SQL: x in (select k from kanji_ids where ids glob '⿰氵*')
- Erq: x in kanji_ids[ids glob '⿰氵*']{k}
9画
- SQL: x in (select k from kanji_strokes where s = 9)
- Erq: x in kanji_strokes[s = 9]{k}
「せ」から始まる
- SQL: x in (select k from kanji_reading where r glob 'せ*' or r glob 'セ*')
- Erq: x in kanji_reading[r glob 'せ*' or r glob 'セ*']{k}

各常用漢字 x についてそれぞれ判定し、複数の条件に当てはまるものを表示すれば作問ができそうです。Erqでクエリを作ってみます。

/* 常用漢字を x という名前で取り出す */
joyo {x: 漢字} distinct
/* 各漢字について、条件を判定する */
{
  x,
  `さんずい`: x in kanji_ids[ids glob '⿰氵*']{k},
  `9画`: x in kanji_strokes[s = 9]{k},
  `「せ」から始まる`: x in kanji_reading[r glob 'せ*' or r glob 'セ*']{k}
}
/* 複数の条件にあてはまる漢字のみ残す */
[`さんずい` + `9画` + `「せ」から始まる` >= 2]
/* あてはまる条件でグループ化 */
{ `さんずい`, `9画`, `「せ」から始まる` => group_concat(x) }
;;

これを入力すると:

erq> /* 常用漢字を x という名前で取り出す */
joyo {x: 漢字} distinct
...> /* 各漢字について、条件を判定する */
...> {
...>   x,
...>   `さんずい`: x in kanji_ids[ids glob '⿰氵*']{k},
...>   `9画`: x in kanji_strokes[s = 9]{k},
...>   `「せ」から始まる`: x in kanji_reading[r glob 'せ*' or r glob 'セ*']{k}
...> }
...> /* 複数の条件にあてはまる漢字のみ残す */
...> [`さんずい` + `9画` + `「せ」から始まる` >= 2]
...> /* あてはまる条件でグループ化 */
...> { `さんずい`, `9画`, `「せ」から始まる` => group_concat(x) }
...> ;;
select `さんずい`, `9画`, `「せ」から始まる`, group_concat(x) from (select x, x in (select k from kanji_ids where (ids glob '⿰氵*')) as `さんずい`, x in (select k from kanji_strokes where (s = 9)) as `9画`, x in (select k from kanji_reading where (r glob 'せ*' or r glob 'セ*')) as `「せ」から始まる` from (select distinct 漢字 as x from joyo) where (`さんずい` + `9画` + `「せ」から始まる` >= 2)) group by (`さんずい`), (`9画`), (`「せ」から始まる`)
["さんずい","9画","「せ」から始まる","group_concat(x)"]
[0,1,1,"宣,専,政,施,星,染,泉,牲,狭,省,窃,背"]
[1,0,1,"清,潜,瀬"]
[1,1,0,"洋,洞,津,洪,活,派,浄,海"]
[1,1,1,"洗,浅"]
4 rows (0.017s)

コマンドラインからクエリを実行する

先ほどは手でクエリを入力していましたが、毎回同じように手で入力するのは面倒なので、次のクエリを kanji-venn.erq ファイルに保存しておき、コマンドで実行してみます。

view temp.kanji_reading = joyo {k: 漢字, r: 音訓};;
view temp.kanji_strokes = mji[漢字施策='常用漢字']{k: 実装したUCS, s: 総画数};;
view temp.kanji_radical = mji[漢字施策='常用漢字'] -:MJ文字図形名:> mji_rsindex -:部首:> radicals {k: 対応するUCS, rad: 部首漢字};;
view temp.kanji_ids = ids[UCS in joyo{漢字}]{k: UCS, ids: IDS} distinct;;
/* 常用漢字を x という名前で取り出す */
joyo {x: 漢字} distinct
/* 各漢字について、条件を判定する */
{
  x,
  p1: x in kanji_ids[ids glob '⿰氵*']{k},
  p2: x in kanji_strokes[s = 9]{k},
  p3: x in kanji_reading[r glob 'せ*' or r glob 'セ*']{k}
}
/* 複数の条件にあてはまる漢字のみ残す */
[p1 + p2 + p3 >= 2]
/* あてはまる条件でグループ化 */
{p1, p2, p3 => group_concat(x)}
;;

npx erq node_modules/@mandel59/mojidata/dist/moji.db < kanji-venn.erq

$ npx erq node_modules/@mandel59/mojidata/dist/moji.db < kanji-venn.erq            
Connected to node_modules/@mandel59/mojidata/dist/moji.db
view temp.kanji_reading = joyo {k: 漢字, r: 音訓};;
view temp.kanji_strokes = mji[漢字施策='常用漢字']{k: 実装したUCS, s: 総画数};;
view temp.kanji_radical = mji[漢字施策='常用漢字'] -:MJ文字図形名:> mji_rsindex -:部首:> radicals {k: 対応するUCS, rad: 部首漢字};;
view temp.kanji_ids = ids[UCS in joyo{漢字}]{k: UCS, ids: IDS} distinct;;
/* 常用漢字を x という名前で取り出す */
joyo {x: 漢字} distinct
/* 各漢字について、条件を判定する */
{
  x,
  p1: x in kanji_ids[ids glob '⿰氵*']{k},
  p2: x in kanji_strokes[s = 9]{k},
  p3: x in kanji_reading[r glob 'せ*' or r glob 'セ*']{k}
}
/* 複数の条件にあてはまる漢字のみ残す */
[p1 + p2 + p3 >= 2]
/* あてはまる条件でグループ化 */
{p1, p2, p3 => group_concat(x)}
;;
create view `temp`.kanji_reading as with kanji_reading as (select 漢字 as k, 音訓 as r from joyo) select * from kanji_reading
ok (0.024s)
create view `temp`.kanji_strokes as with kanji_strokes as (select 実装したUCS as k, 総画数 as s from mji where (漢字施策 = '常用漢字')) select * from kanji_strokes
ok (0.000s)
create view `temp`.kanji_radical as with kanji_radical as (select 対応するUCS as k, 部首漢字 as rad from mji join mji_rsindex on mji.MJ文字図形名 = mji_rsindex.MJ文字図形名 join radicals on mji_rsindex.部首 = radicals.部首 where (漢字施策 = '常用漢字')) select * from kanji_radical
ok (0.000s)
create view `temp`.kanji_ids as with kanji_ids as (select distinct UCS as k, IDS as ids from ids where (UCS in (select 漢字 from joyo))) select * from kanji_ids
ok (0.000s)
select p1, p2, p3, group_concat(x) from (select x, x in (select k from kanji_ids where (ids glob '⿰氵*')) as p1, x in (select k from kanji_strokes where (s = 9)) as p2, x in (select k from kanji_reading where (r glob 'せ*' or r glob 'セ*')) as p3 from (select distinct 漢字 as x from joyo) where (p1 + p2 + p3 >= 2)) group by (p1), (p2), (p3)
["p1","p2","p3","group_concat(x)"]
[0,1,1,"宣,専,政,施,星,染,泉,牲,狭,省,窃,背"]
[1,0,1,"清,潜,瀬"]
[1,1,0,"洋,洞,津,洪,活,派,浄,海"]
[1,1,1,"洗,浅"]
4 rows (0.032s)

2022-08-12

簡単関係照会言語 Erq で快適なデータベース分析生活を送る

プログラミング

Erq（アーク）は、SQLの代わりにアドホックなデータ分析に用いることを主目的とした、新しいデータベース言語です。リレーショナルデータベースは便利ですが、アドホックなデータ分析を行う上で、SQLの文法は面倒なものです。Erqは、SQLのセマンティクスは極力そのままに異なる文法を採用することで、簡単にクエリを書けるようになっています。

SQLクエリの実例

私はSQLiteデータベースに漢字の文字情報を入れて、複雑な検索や分析ができるようにしているのですが、実際にそのデータベースを使ったクエリ例を見てみましょう。使っているMojidataデータベースは、次のリポジトリからビルドできます。

GitHub - mandel59/mojidata: Character Database for CJKV Text Processing

まず、漢字の読みを集めたmji_readingテーブルの内容を全部表示するために、SQLで次のように照会します。（末尾のセミコロン ; は、SQLite CLIにおける文の終端記号です。）

select * from mji_reading;

データは全部で122148件あるのですが、冒頭のデータはこんな感じになっています。MJ文字図形名は、文字情報基盤における図形番号です。

"MJ文字図形名","読み"
MJ000001,"おなじ"
MJ000001,"くりかえし"
MJ000001,"のま"
MJ000002,"しめ"
MJ000004,"キュウ"
MJ000004,"おか"
MJ000005,"テン"
MJ000006,"キ"
MJ000006,"よろこぶ"
MJ000007,"カ"

ここで、簡単な分析として、読みごとに件数をカウントし、多い順に10件表示してみましょう。

select 読み, count(*) from mji_reading group by 読み order by count(*) desc limit 10;

"読み",count(*)
"コウ",2775
"ショウ",1985
"ソウ",1732
"シ",1730
"トウ",1675
"キ",1536
"カン",1515
"セン",1476
"キョウ",1437
"ケン",1279

カラムを追加し、読みに対応する漢字の例をいくつか表示してみましょう。mji_readingに格納されているのはUnicodeではなくMJ文字図形名なので、Unicodeの漢字を表示するには、別のテーブル mji と結合して照会する必要があります。UnicodeとMJ文字図形名は1対多対応なので、重複するUnicodeを排除するために、select句にdistinctキーワードを使います。また、表示する漢字を最大5つに制限するために、サブクエリを二重に使って、limit句で制限をかけたデータに対してgroup_concat()集約関数で集約を行うことにします。そうすると、クエリはこのようになります。

select
  読み,
  count(*),
  (
    select group_concat(c)
    from (
      select distinct 対応するUCS as c
      from mji
      natural join mji_reading as r
      where r.読み = mji_reading.読み
      limit 5
    )
  ) as 例
from mji_reading
group by 読み
order by count(*) desc
limit 10;

"読み",count(*),"例"
"コウ",2775,"㐬,㒶,㓂,㓚,㓛"
"ショウ",1985,"㐮,㐮,㐼,㑱,㒉"
"ソウ",1732,"㐮,㑿,㒎,㔌,㔿"
"シ",1730,"㑥,㒋,㒾,㓨,㓼"
"トウ",1675,"㑽,㓊,㓱,㓸,㔁"
"キ",1536,"㐂,㑧,㑶,㒫,㔳"
"カン",1515,"㒈,㓧,㔋,㔶,㖤"
"セン",1476,"㑒,㒄,㒨,㒰,㔊"
"キョウ",1437,"㐩,㓋,㓏,㓙,㕳"
"ケン",1279,"㐸,㒽,㓩,㓺,㔓"

上記の例は単純ですが、SQLの冗長性・煩雑性がよく表れています。

select句とgroup by句やorder by句に重複して書くことになる。
select句はクエリの先頭、group by句やorder by句はクエリの末尾にあるので、カーソル移動が面倒くさい。
サブクエリにも都度selectキーワードを書くので、多重のサブクエリは記述量がすごく多くなってしまう。
処理の流れ上は後にくるselect句が先頭にあるので、処理の流れがクエリ上で行ったり来たりしてしまう。
テーブル名やカラム名の別名を式の後に書くので、後から読むとき、特に長い式の場合に、見づらい。

Erqクエリの実例

今度は同じ分析をErqで行ってみましょう。テーブルの全件取得は、Erqではテーブル名を書くだけです。（Erq CLIでは、文の終端記号に";;"を使っています。）

mji_reading;;

読みごとに件数をカウントし、多い順に10件表示するには、次のように書きます。

mji_reading {読み => count(*) desc} limit 10;;

ブレース・アロー記法 { ... => ... } はErqにおける集約クエリの書き方で、アローの左側にグループに使うカラムを、アローの右側に集約関数のカラムを書きます。また、カラムの後に asc/desc を指定することもできます。この記法によって、SQLのselect句・group by句・order by句の指定を一度に行えるので、Erqでは集約を書くのが簡単になっています。

サブクエリはどうでしょうか。SQLのときと同様に、漢字の例のカラムを追加してみます。

mji_reading
{
  読み =>
  count(*) desc,
  例:
    from mji
    natural join r: mji_reading
    [r.読み = mji_reading.読み]
    {c: 対応するUCS}
    distinct
    limit 5
    {group_concat(c)}
}
limit 10;;

Erqでは、サブクエリの先頭にfromを書きます。サブクエリを括弧で括る必要はありません。（トップレベルのクエリにもfromをつけて良いのですが、省略できます。サブクエリではテーブル名とカラム名の区別のため、基本的にはfromキーワードが必要です。）
カラム名やテーブル名の別名は、式の前に書きます。
ブラケット記法 [...] はwhere句・having句に相当します。
ブレース記法 {...} はselect句に相当しますが、from句の後に書きます。
distinctキーワードは、Erqでは独立したdistinct句です。
ブラケット記法やブレース記法は、クエリに複数書いても問題ありません。

Erqのこれらの特徴により、SQLでは二重のサブクエリとして書いていたクエリを、すっきりとした直列的なサブクエリとして記述できました。

そのほかのクエリ例

他にもいくつかクエリ例を載せてみます。Erq CLIではErqクエリから変換されたSQLを出力するので、どういう変換が行われるか分かるようになっています。

ブラケット記法がhaving句に変換される例

erq> unihan_variant[property='kTraditionalVariant']{s: UCS => t: group_concat(value, '')}[count(*)>1] limit 10;;
select UCS as s, group_concat(value, '') as t from unihan_variant where (property = 'kTraditionalVariant') group by (UCS) having (count(*) > 1) limit 10
["s","t"]
["䴘","鷈鷉"]
["䴙","鷿鸊"]
["么","幺麼麽"]
["云","云雲"]
["伪","偽僞"]
["余","余餘"]
["冲","沖衝"]
["出","出齣"]
["历","曆歷"]
["发","發髮"]
10 rows (0.015s)

共通テーブル式とユニオン

erq> with t(a, b) as (`kdpv_cjkvi/non-cognate`{subject, object}) (t{a, b}; t{b, a}) join unihan_kTotalStrokes on a = UCS {a, b, s: cast(value as integer) asc}[s = 1];;
with t(a, b) as (select subject, object from `kdpv_cjkvi/non-cognate`) select a, b, cast(value as integer) as s from (select a, b from t union all select b, a from t) join unihan_kTotalStrokes on a = UCS where (s = 1) order by (cast(value as integer)) asc
["a","b","s"]
["乀","乁",1]
["乀","乁",1]
["乁","乁",1]
["乙","𠃉",1]
["乁","乀",1]
["𠃉","乙",1]
["乁","乀",1]
["乁","乁",1]
8 rows (0.015s)

共通テーブル式を使った再帰クエリ

erq> with g(i) as ({i: 1}; g{i + 1} limit 10) g;;
with g(i) as (select 1 as i union all select i + 1 from g limit 10) select * from g
["i"]
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
10 rows (0.000s)

再帰クエリを使ってグラフを辿る

erq> with v(a, b) as (mjsm natural join mji {対応するUCS, 縮退UCS})
...> with w(a, b) as (v; v{b, a})
...> with g(a, b) as ({null, '刈'}; g join w on g.b = w.a {w.a, w.b} distinct)
...> g {a => group_concat(b)};;
with v(a, b) as (select 対応するUCS, 縮退UCS from mjsm natural join mji), w(a, b) as (select * from v union all select b, a from v), g(a, b) as (select distinct null, '刈' union select distinct w.a, w.b from g join w on g.b = w.a) select a, group_concat(b) from g group by (a)
["a","group_concat(b)"]
[null,"刈"]
["㓼","刹"]
["㔑","刹"]
["䒳","䒳,朵,朶,𣎾,𣎿,𣏻"]
["䓭","刹,苅"]
["刈","刈,苅,𠚫,𠛄,𭃅,𭃆"]
["刴","刹,朶"]
["刹","㓼,㔑,䓭,刴,刹,剎,𠛴,𠞻"]
["剎","刹"]
["朵","䒳,朶"]
["朶","䒳,刴,朵,朶,𣎾,𣎿,𣏻"]
["苅","䓭,刈,苅,𠛄,𫟌"]
["𠚫","刈"]
["𠛄","刈,苅"]
["𠛴","刹"]
["𠞻","刹"]
["𣎾","䒳,朶"]
["𣎿","䒳,朶"]
["𣏻","䒳,朶"]
["𫟌","苅"]
["𭃅","刈"]
["𭃆","刈"]
22 rows (0.123s)

in演算子とorder by句の例

erq> mji natural join mji_reading[対応するUCS in joyo{漢字}]{漢字: 対応するUCS => 読み: group_concat(distinct 読み)} order by count(distinct 読み) desc limit 10;;
select 対応するUCS as 漢字, group_concat(distinct 読み) as 読み from mji natural join mji_reading where (対応するUCS in (select 漢字 from joyo)) group by (対応するUCS) order by count(distinct 読み) desc limit 10
["漢字","読み"]
["明","メイ,ミョウ,ミン,ベイ,ボウ,あかり,あかるい,あかるむ,あからむ,あきらか,あける,あく,あくる,あかす,ひかり"]
["生","セイ,ショウ,ソウ,いきる,いかす,いける,うまれる,うむ,おう,はえる,はやす,き,なま,うぶ"]
["行","コウ,ギョウ,アン,ゴウ,カン,ガン,いく,ゆく,おこなう,まさに,みち,めぐる,やる,ゆくゆく"]
["上","ジョウ,ショウ,うえ,うわ,かみ,あげる,あがる,のぼる,のぼせる,のぼす,たっとぶ,たてまつる,ほとり"]
["下","カ,ゲ,ア,した,しも,もと,さげる,さがる,くだる,くだす,くださる,おろす,おりる"]
["白","ハク,ビャク,ベ,ハ,ヒャク,シ,ジ,しろ,しら,しろい,しらげる,しらむ,もうす"]
["薄","ハク,ヘキ,ホ,うすい,うすめる,うすまる,うすらぐ,うすれる,せまる,すすき,バク,ビャク,ブ"]
["重","ジュウ,チョウ,ジュ,ズ,トウ,シュウ,シュ,え,おもい,かさねる,かさなる,おもんじる,はばかる"]
["反","ハン,ホン,タン,ヘン,ベン,そる,そらす,かえす,かえって,かえる,そむく,たん"]
["懐","カイ,エ,ふところ,なつかしい,なつかしむ,なつく,なつける,いだく,おもい,こころ,おもう,ふところにする"]
10 rows (0.021s)

ローバリュー演算

erq> with u(s, t) as (unihan_variant[property='kTraditionalVariant']{UCS, value})
...> u[{s, t} not in tghb_variants{规范字, 繁体字}] limit 10;;
with u(s, t) as (select UCS, value from unihan_variant where (property = 'kTraditionalVariant')) select * from u where ((s, t) not in (select 规范字, 繁体字 from tghb_variants)) limit 10
["s","t"]
["㐷","傌"]
["㐹","㑶"]
["㐽","偑"]
["㑈","倲"]
["㑔","㑯"]
["㑩","儸"]
["㑺","儁"]
["㓥","劏"]
["㔉","劚"]
["㖊","噚"]
10 rows (0.006s)

Erq実装について

現状はNode.js/JavaScriptでSQLiteのErqクライアントを実装し、個人的に利用しています。

GitHub - mandel59/erq

将来的にはRustなどで実装しなおすかもしれませんが、現状でもそれなりに便利に使えています。リポジトリには公開していないので、GitHubからインストールしてください。次のコマンドを実行すると、erqコマンドがインストールされます。

npm install -g github:mandel59/erq

2020-11-11

漢字処理に使うデータベース・関連サイトまとめ

漢字技術プログラミング

Unicode Character Database www.unicode.org

Ideographic Variation Database unicode.org

Adobe-Japan1 github.com

MJ文字情報一覧表 mojikiban.ipa.go.jp

漢字データベース kanji-database.sourceforge.net

GlyphWiki glyphwiki.org

萌典 www.moedict.tw

2019-09-02

TopShell: シェル再考

プログラミング

GitHubのExplore repositoriesにたまたま表示されていた TopShell が気になったので、ここで紹介する。

github.com

TopShell開発の動機は TopShell: Reimagined Terminal and Shell · topshell-language/topshell Wiki · GitHub に書いてあるが、要点をまとめると「古典的なUnixシェルを使うのはつらい。いいところだけを抜き出して、全くシェルを考えたら、どうなるだろうか？」ということらしい。

Unixシェルのだめなところ
- 未定義の変数を使ってもエラーにならない【デフォルトで。set -u を使えばエラーになる。】
- コマンドがエラーになってもスルーされる【デフォルトで。set -e とか set -opipefail を使えばエラー時に中断される。】
- 全部のデータが文字列
  - sed や awk の不思議なコードを覚えないといけない
  - 不完全なパーサーを書いて処理することになる
Unixシェルのいいところ
- システムへの実用的でインタラクティブなインターフェースを提供している
- パイプを使ってコマンドを合成することで、素早く問題を解決できる
TopShell
- 純粋計算と作用（副作用）を分離する純粋関数型プログラミング
- モダンな型システム
- 細かいコード断片を書けば、直ちに評価され、結果を見ることができる
  - 結果はテキストのみならず、画像でもアニメーションでもよい
- 非同期タスクとリアクティブストリームによるプログラムの合成
- これらを努力なしに使うことができる環境

理屈はともかく、TopShellはブラウザから使うことができる。次のリンクからプレイグラウンドを開いて、試してみよう。

http://show.ahnfelt.net/topshell/

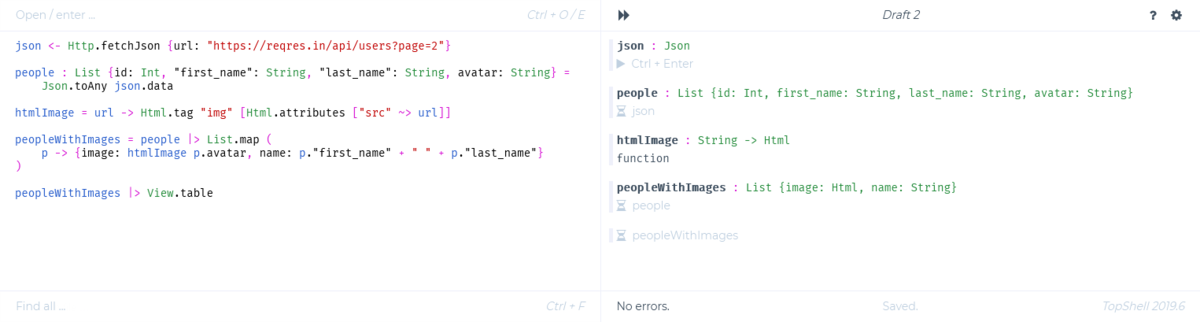
https://github.com/topshell-language/topshell#http-example のサンプルコードを画面左側のエディタに入力すると、直ちに評価結果が右側に表示される。といっても、副作用が発生するタスクやストリーム（バインド文 x <- e で宣言されているもの）は、行にカーソルをあわせて Ctrl + Enter で1文ずつ実行するか、実行ボタンを押すまでは実行されない。感覚的には、シェルというより Jupyter Notebook に近い気もする。

json <- Http.fetchJson {url: "https://reqres.in/api/users?page=2"}

people : List {id: Int, "first_name": String, "last_name": String, avatar: String} = 
    Json.toAny json.data

htmlImage = url -> Html.tag "img" [Html.attributes ["src" ~> url]]

peopleWithImages = people |> List.map (
    p -> {image: htmlImage p.avatar, name: p."first_name" + " " + p."last_name"}
)

peopleWithImages |> View.table

f:id:mandel59:20190902225844p:plain — HTTP example

f:id:mandel59:20190902230537p:plain — HTTP exampleの実行結果

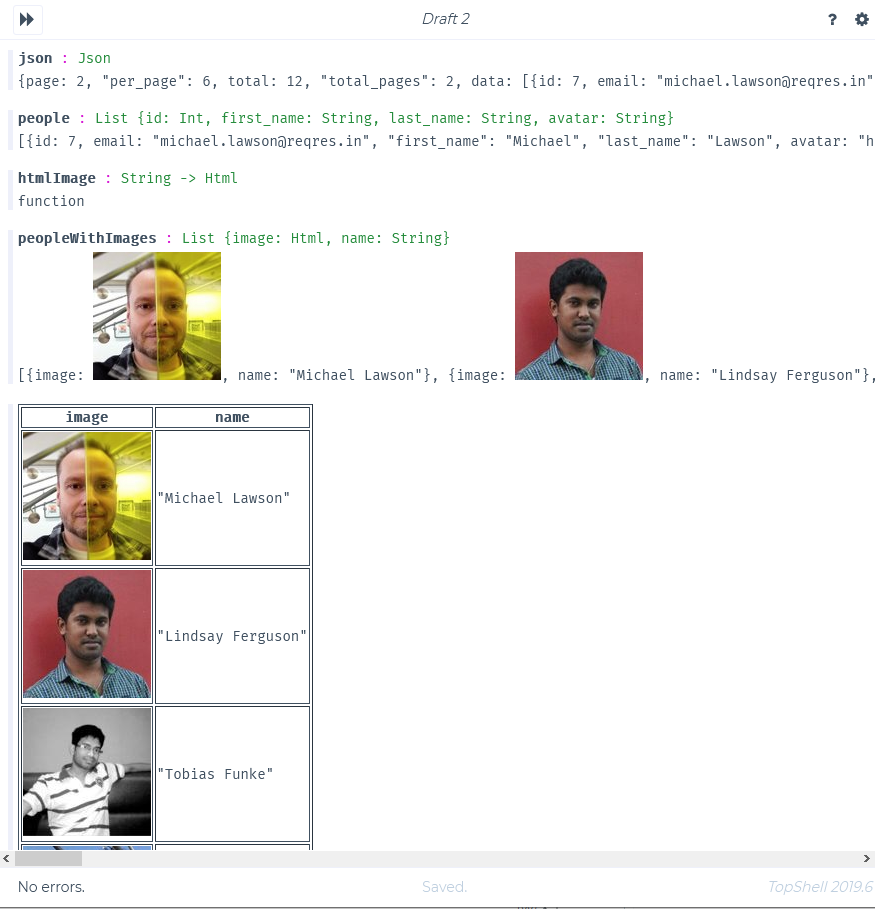
ストリームのサンプルとして https://github.com/topshell-language/topshell#stream-example も試してみよう。この例では、時計のアニメーションが動く。

言語仕様についてはまた今度書く。

2019-03-24

位置の外延的表現・内包的表現の区別と考察ノート

プログラミング哲学技術

オブジェクトの位置の表現方法には、大きく分けて2種類ある。ここではそれを、外延的表現と内包的表現と呼びわけ、ボードゲームの駒の位置の表現を具体例にして、どのような違いがあるかを考えてみる。

今、将棋盤上においてある、王将の位置を表したい。どのような表現が考えられるか。（王将なので、手駒や成りについては考えないこととする。）

ひとつは、将棋盤を2次元配列として用意し、駒の位置に該当する要素として、駒の識別子を代入するものが考えられる。

// コード1
let 将棋盤 = Array.from({ length: 9 }, () => Array.from({ length: 9 }, () => null))
将棋盤[8][4] = "王将"

コード1を実行した結果、 将棋盤 は次のような配列になる。駒の位置は、将棋盤配列上の特定の要素として駒を表す識別子 "王将" を格納することで表現している。このような表現方法を、位置の外延的表現と呼ぶことにする。

[ [ null, null, null, null, null, null, null, null, null ],
  [ null, null, null, null, null, null, null, null, null ],
  [ null, null, null, null, null, null, null, null, null ],
  [ null, null, null, null, null, null, null, null, null ],
  [ null, null, null, null, null, null, null, null, null ],
  [ null, null, null, null, null, null, null, null, null ],
  [ null, null, null, null, null, null, null, null, null ],
  [ null, null, null, null, null, null, null, null, null ],
  [ null, null, null, null, "王将", null, null, null, null ] ]

これは 将棋盤[8][4] == "王将" である点で次の表現と大差ないので、簡潔にこちらを使って考えてもよい。

{ "8": { "4": "王将" } }

もうひとつの方法では、将棋盤を連想配列として用意し、駒に該当する要素として、駒の座標を代入する。

// コード2
let 将棋盤 = {}
将棋盤["王将"] = [4, 8]

コード2を実行した結果、 将棋盤 は次のようなオブジェクトになる。駒の位置を座標で表現するこの方法を、位置の内包的表現と呼ぶことにする。

{ "王将": [4, 8] }

位置の外延的表現と内包的表現の違いですぐ分かるのは、配列の添字と要素の関係が入れ替わっていることだ。外延的表現では、座標が添字、識別子が要素となっている。一方、内包的表現では識別子が添字、座標が要素だ。

このことは、情報へのアクセスの容易さと関わってくる。外延的表現では、位置からオブジェクトを得ることは簡単だが、オブジェクトの位置を得るには配列をスキャンしなければならない。内包的表現ではその逆で、オブジェクトの位置はすぐ分かるが、どの位置に何があるかは、オブジェクト全体をスキャンする必要がある。両方向での参照を高速に行うために、場合によっては、索引を作る必要が出てくる。

アクセスの容易さの他に、添字の空間の違いもある。外延的表現では添字が座標なので、2次元配列を使っている。一方、内包的表現では添字が識別子であるため、連想配列を使っている。つまり、添字の空間構造次第で、使うべきコンテナデータ構造が異なってくる。配列や連想配列を言語機能として備えている言語は多いが、添字空間が広大だったり連続的であるならば、R木のような構造が必要な場合もあるだろう。

オブジェクト指向のデータ表現では、オブジェクトを基準にデータが凝集されるため、素朴に設計すると内包的表現を選びがちではないかという気がする。しかし、それは空間上の現象を上手く表現することが難しいという問題がある。空間上で隣り合ったオブジェクトに作用するといった処理を書くには、将棋盤というオブジェクトを意識し、外延的表現を使う必要が出てくる。

2018-10-16

昔作ったリポジトリがフォークされていた話

プログラミング TypeScript

昔、SQLiteをWebAssembly向けにビルドする例をGitHubに置いていたんだけど、 github.com

先月ごろフォークされて Uno.sqlite-wasm というリポジトリができていた。 github.com

Unoは、UWPアプリをiOSやAndroid, WebAssembly上で動かすプラットフォームらしい。

github.com

デモも公開されている。

The SQLite + Entity Framework Core App, a demo of the combination of Roslyn, Entity Framework Core, SQLite and the Uno Platform to manipulate an in-browser database.

https://github.com/nventive/Uno#live-webassembly-apps

練習で作ったリポジトリだったので、ドキュメントやコメントはほぼ無かったのに、よく拾い上げてハックしたな、と思った。まあ、シンプルな構成だからドキュメントがなくても理解できるとも思う。

（当のsqlite-wasm, TypeScriptで書いた部分には微妙なこだわりを出していて、普通に型を付けたらポインタが全部number型になるのを避けるために、前回紹介したPhantom property patternを使っていたりする。）

2018-09-01

Phantom property pattern

プログラミング TypeScript

TypeScriptは、JavaScriptエンジンの動的セマンティクス上に、静的な型システムのセマンティクスが重なっているものです。ここで、JavaScriptとしては正しく実行できても、TypeScriptの型システム上ではちゃんと型が付かないという場合もあります。ときには、TypeScriptで型がつくように大幅に書き換えないといけない場合も出てきたりして、そうなると大変です。それでも、TypeScriptの型システムは高度な機能を持っているので、大体の場合は、うまく表現してやると、JavaScriptらしい書き方のままで型をつけることができてしまいます。今回は、JavaScriptでよくある、プリミティブ値をそのまま取り回すパターンに型を付けたいと思います。

プリミティブ型を扱うプログラミングは、素朴でわかりやすいですが、型の考えからするとかなり悪いものです。こういうプログラミングを行うと、あらゆるデータを文字列で表す様子から、ときに”stringly typed”と揶揄されます。文字列は、表したいものはとりあえず何でも表現できるのでとても便利ですが、いろいろな種類のデータが一つの型で表されてしまうのなら、型が役立たずになってしまいます。すべてがstring型のプログラムで、どうやってその文字列の中身がテキストなのか、URLなのか、メールアドレスなのかを判断するのでしょうか？文脈を読み込んで察するか、ハンガリアン記法に回帰するか、さもなくばエスパーで当てるしかないでしょう。

この問題に対処するひとつの「まっとうな」方法は、プリミティブ値を直接使わず、適宜ラッパーオブジェクトを作り、その上でプログラミングを行うことでしょう。プリミティブ値ではなくオブジェクトを使えば、メソッドを追加することも容易です。しかし、実際にJavaScriptでそういうことが行われづらい原因として、ひとつはプリミティブ値をコンストラクタでラップするが手間だという点、ひとつは===による同一性比較がオブジェクト型に対しては工夫を加えなければ意味上の同値性比較にならない点、ひとつは性能上の問題点、ひとつはシリアライズ・デシリアライズの自明さが失われる点が挙げられます。要するに、プリミティブ値をオブジェクトで包むのはわりとデメリットもあるわけです。

今ここに、この問題へのもうひとつの対処方法、幽霊プロパティパターン phantom property pattern を提唱します。このパターンを使うと、プリミティブ値の型を好きなだけ定義できる。つまり、言語組み込みのプリミティブ値を取り回すプログラムでありながら、各プリミティブ値を別々の型として取り扱うことができるようになります。

幽霊プロパティパターンでは、まず、次のような型を定義します。

export type Tag<X, R extends keyof any, Y> = X & {
    [rel in R]: Y
}

x: Tag<X, R, Y>は「xはXで、xのRはYである」というような意味になります。

次に、幽霊シンボルを定義します。

// This is a phantom symbol, which does not exist at run time
declare const _unit: unique symbol
export type unit = typeof _unit

_unitは幽霊シンボルで、宣言しますが、実際には定義しません。_unitの型はユニークシンボル型ですが、このままでは型に名前がなく使いづらいので、unitというエイリアス名を付けます。

ここに定義したTag型コンストラクタと幽霊シンボルを組み合わせると、プリミティブ値の性質を幽霊プロパティとして表現できます。

例として、角度の単位を幽霊プロパティとして付加した型を定義してみましょう。

export type Scale<X, U> = Tag<X, unit, U>
export type Radian = Scale<number, "radian">
export type Degree = Scale<number, "degree">

ここで定義したRadian, Degreeは両方ともプリミティブ値の数値を元とする型ですが、実際には存在していない[_unit]プロパティの型が異なるため、相互に代入不可能となっています。

{
    const x: Degree = 30 as Degree
    const y: Radian = x // type error!
    console.log(x, y)
}

いいですね。これを使って、たとえば三角関数や双曲線関数に単位をつけてあげるといい感じになります。

export const sin = Math.sin as (x: Radian) => number
export const tanh = Math.tanh as (x: Radian) => number
export const asin = Math.asin as (x: number) => Radian
export const atanh = Math.atanh as (x: number) => Radian

{
    const x = 30 as Degree
    const y = sin(x) // type error!
    console.log(y)
}

弧度法で渡すべきところをうっかり度数法で渡すミスを、これで防げますね。相互に変換する関数も用意してあげましょう。

// Ref: https://tauday.com/tau-manifesto
const τ = 2 * Math.PI

/** converts radian to degree */
export function toDegree(x: Radian): Degree {
    return (x / τ * 360) as Degree
}

/** converts degree to radian */
export function toRadian(x: Degree): Radian {
    return (x / 360 * τ) as Radian
}

{
    const x = 30 as Degree
    const y = sin(toRadian(x)) // ok
    console.log(y)
}

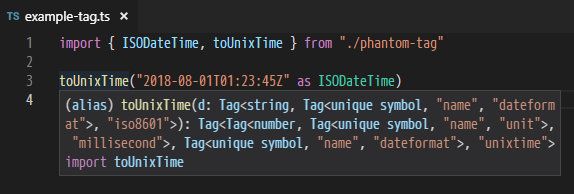
例をもう一つ、今度はUnix時間とISO8601を扱ってみます。今度は単位ではなくデータフォーマットの話なので、新しくdataformat型を定義しています。

declare const _dataformat: unique symbol
export type dataformat = typeof _dataformat

export type UnixTime = Tag<Unit<number, "millisecond">, dataformat, "unixtime">
export type ISODateTime = Tag<string, dataformat, "iso8601">
export const now = Date.now as () => UnixTime
export const toISODateTime = (t: UnixTime): ISODateTime => new Date(t).toISOString() as ISODateTime
export const toUnixTime = Date.parse as (d: ISODateTime) => UnixTime
export function isISODateTime(s: string): s is ISODateTime {
    return /^\d{4}-\d{2}-\d{2}T\d{2}:\d{2}:\d{2}(?:\.\d{1,3})?Z$/.test(s)
}

{
    const t = 1514810096000 as UnixTime
    console.log(toISODateTime(t))
    const d = "2018-01-01T12:34:56Z"
    if (isISODateTime(d)) {
        console.log(toUnixTime(d))
    }
}

UnixTime型はデータフォーマットだけでなく、単位も幽霊プロパティで付加していますね。一口にUnix時間と言っても、実際にはミリ秒単位のものと秒単位のものが混ざっていることがよくあるのですが、こういう工夫が事故を防いでくれるはずです。

ISODateTime型の方は、型ガード関数を用意しました。こういう関数を用意して使うほうが、直接as ISODateTimeでダウンキャストするよりも安全です。

欠点

本当ならinterface Tag<X, R, Y> extends X { [rel in R]: Y }とでも定義したいところですが、現状のTypeScriptではプリミティブ型を拡張できないため、やむなく交叉型 intersection type で表現しています。
幽霊シンボルそれ自体はexportしないほうがいいでしょう。実在しない識別子なので、アクセスしても型エラーになりませんが実行時エラーになる可能性があります。型レベルで使うだけでシンボル自体はなくてもいいので、シンボルの型に名前を付けて、そちらをexportするといいです。
interfaceではないため、スニペットやコンパイラのエラーメッセージ等で、型エイリアスが展開されて表示されてしまいます。unique symbolと表示されるだけなのは非常にまずいです。
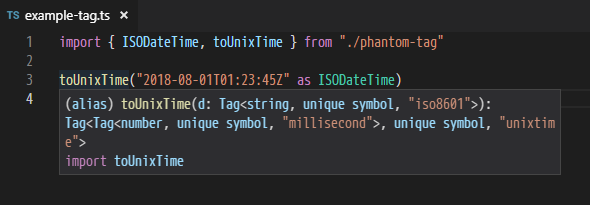
- ワークアラウンドとして、幽霊シンボル自体にタグをつけるように書き換えると、なんとか分かるようになります。

declare const _unit: unique symbol
export type unit = Tag<typeof _unit, "name", "unit">
export type Unit<X, U> = Tag<X, unit, U>

declare const _dataformat: unique symbol
export type dataformat = Tag<typeof _dataformat, "name", "dateformat">

まとめ

幽霊プロパティパターンを使うと、実行時コストに影響を与えることなく（ゼロコストで）、プリミティブ値にユーザー定義の型をつけることができるようになります。

2019/08/20追記: この記事を書いた時点では、先行事例があるということをちゃんと調査していませんでしたが、実は"Branding"と呼ばれて、それなりに使われている技法であることを知りました。（TypeScriptのソースコードでも使われています。）

以下の記事では、Brandingや、その変形であるFlavoringについて解説されています。 Need Flexible Nominal Typing for TypeScript? Use Flavoring, not Branding

2016-12-17

「What Is Functional Programming? に対する反論」を読んで考えたこと

プログラミング

lyrical-logical.hatenablog.com

読んでいて引っかかった部分について考えました。

mutable変数は「入力とは呼べない」？

この記事で僕が伝えたいのは、君が書くあらゆる関数には二組の入力と二組の出力があるってことだ。

間違いなく、InboxQueue の状態はこの関数の本物の入力だ。

この隠れた入出力にはちゃんとした名前があって、その名を「副作用」という

InboxQueue は、その関数スコープから参照可能な変数の一つに過ぎない。たまたまその関数の環境から触れるというだけで、入力というよりは、環境の中の mutable な変数の一つ、以上のことはないし、これを入力とは呼べない。これはプログラムの状態だ。
http://lyrical-logical.hatenablog.com/entry/2016/12/15/135831

問題のプログラムはこれです。

public void processNext() {
    Message message = InboxQueue.popMessage();

    if (message != null) {
        process(message);
    }
}

これはJavaのコード断片ですけど、断片だと分かりづらいので、JavaScriptでプログラム全体を書いてみることにします。

let Processor = {
  inbox: null,
  console: null,
  processNext() {
    let message = this.inbox
    if (message != null) {
      this.console = message
    }
  }
}

function main() {
  Processor.inbox = "hello"
  Processor.processNext()
  console.log(Processor.console)
}

main()

このコードのprocessNextメソッドは、元のコード断片より簡略化されているけど、議論の要点はおさえているはずです。

確かに、Processor.inboxはProcessor.processNextメソッドから参照可能なmutableプロパティですが、同時にmain関数からも参照可能です。このことが、mutableプロパティを一種の「共有メモリ」として使った2関数間の通信を可能にしています。

プロパティ経由の値の受け渡しが、「プログラムの状態」としてプログラミング言語のセマンティクス内で説明できる動作だとしても、Processor.inboxはProcessor.processNextへの入力となっていると表現して問題ないはずです。

このコード例から、次のことが言えます:

関数の外部から書き換え可能で、関数の内部から参照可能なmutable変数は、関数への入力として使うことができる。（このような入力を副原因という。）
関数の内部から書き換え可能で、関数の外部から参照可能なmutable変数は、関数からの出力として使うことができる。（このような出力を副作用という。）

副原因と副作用は対称的で、Processor.inboxはProcessor.processNextにとって副原因の源ですが、mainにとっては副作用の対象です。つまり、副原因があるとき、対になる副作用も現れ、大域的に見れば両者は同一の現象です。

「暗黙的に環境内の変数を参照するよりも、陽に変数を取るようにしたほうがいい」？

言いたいことは分かる。暗黙的に環境内の変数を参照するよりも、陽に変数を取るようにしたほうがいい。
public void processNext(InboxQueue inboxQueue) {
    Message message = inboxQueue.popMessage();

    if (message != null) {
        process(message);
    }
}
http://lyrical-logical.hatenablog.com/entry/2016/12/15/135831

環境に依存した関数の定義には注意すべし、それは一般に言って正しいことだと思うし、反論するつもりはない。しかしそれを「関数型プログラミングって何？」という文脈で話すのは、違和感が強い。
http://lyrical-logical.hatenablog.com/entry/2016/12/15/135831

ここで言っている「環境」って、何を指しているんでしょうか？グローバル環境のことでしょうか？それとも、関数の引数ではなく、ブロックスコープに宣言された変数を、環境内の変数と呼んでいるのでしょうか？あるいは、次のようなクロージャーで、関数g内で参照されているxはgの引数ではないわけですけど、こういう場合も「暗黙的に環境内の変数を参照する」に入るんでしょうか？

function f(x) {
  return function g(y) {
    return x + y
  }
}

「あらゆる関数」？

しかし * あらゆる * 関数に二つの入力がある、と記事では主張している。つまり上のコードでは不足だろう。
ならもうちょっと別の書き方をしよう。コードは疑似的なもので、こんな API がある言語は知らない。
public void processNext(Frame frame) {
    Message message = ((InboxQueue)frame.getEnvironment.getVariables.searchVariable("InboxQueue")).popMessage();

    if (message != null) {
        process(message);
    }
}
あるいは、InboxQueue の状態をある種の precondition としてとってもいいかもしれない。
public void processNext(InboxQueueState state) {
    // state を使って何かしたいときもあるかもしれない。以下は一例だ。関数の意味は変わる。元記事では関数の前提条件について何も触れられていないので、これは自分が勝手に加えたものだ。popMessage は blocking API かもしれないし、そうであればこのような前提条件は妥当でない。
    if (state.isEmpty()) throw new IllegalArgumentException("InboxQueue must has some elements.");
    // これは assert を書いて precondition をコード上で陽にしているのと大した差はない。
    assert(!state.isEmpty());

    Message message = InboxQueue.popMessage();

    if (message != null) {
        process(message);
    }
}
一歩譲って、これらをもってして、あらゆる関数には二つの入力がある、という主張を受け入れたとしよう。しかしそれは「関数プログラミングにとって」大事なことなんだろうか。
http://lyrical-logical.hatenablog.com/entry/2016/12/15/135831

このくだりはほとんど意味が分かりません。「関数型プログラミングって何？」の酷さを示すために、書かれたとおりにやってみて酷さを示すというにしては、そもそも書いてもいないことを突然やりだしたように見えます。「上のコードでは不足だろう」と思った理由もはっきりしなければ、それで例に出した「別の書き方」をそう書いてみたワケも、書かれていません。

“I put it to you that every function you write has two sets of inputs and two sets of outputs.” という一文中の “every” という一語が気にくわないということ以上ではないのであれば、よく分からない例なんか出さずとも、記事最初の例

public int square(int x) {
    return x * x;
}

には副原因も副作用もないよね、と指摘すれば済むのでは、と思ってしまいます。

でも、ただ「 * あらゆる * 関数に」って書き方じゃなくてevery function you writeなんだし、自分はこれは記事に食い付かせる「釣り」のたぐいの表現なんじゃないでしょうか。まあ、こういう正確さに欠けた表現はちょっと気に障るってのは分かります。

「本当にそうだろうか」？

これで、この関数は入力（や出力）を隠し持たなくなった。

本当にそうだろうか。上の主張は関数内で読んでいる関数が純粋であるという仮定が成り立つときに限る。"getSchedule" "programAt" が純粋でないなら、そこには状態が潜んでいる。関数内で呼び出している関数のスコープにある状態に触れている、依存している可能性がある。
http://lyrical-logical.hatenablog.com/entry/2016/12/15/135831

もう少し前に、こう書いてあります。

この関数には現在時刻 (new Date()) という入力が隠れている。
http://okapies.hateblo.jp/entry/2016/12/15/021550

"getSchedule" "programAt" が純粋でないなら、「この関数には現在時刻 (new Date()) という入力が隠れている」という部分で一緒に副作用（あるいは副原因）のある関数としてリストアップされなければ、話の構造上不自然です。ここでリストアップされていない以上、 "getSchedule" "programAt" は純粋だということが暗に示されてます。それを、陽に示されていないからといって「"getSchedule" "programAt" が純粋でないなら」と言い出すのは、揚げ足取りに見えます。

「一般的な説明でよいだろう」？

引数にのみ依存し値を返す、同じ引数に対して常に同じ値を返す関数であるという一般的な説明でよいだろう。
http://lyrical-logical.hatenablog.com/entry/2016/12/15/135831

「引数にのみ依存し値を返す、同じ引数に対して常に同じ値を返す関数」という定義には問題があります。この定義では、副原因を持たないが副作用を持つ、次のような関数を除外できないのでダメです。*1

let a = null

function out(x) {
  a = x
  return x
}

「読めば訳された記事がイマイチなのは分かる」？

結論。住井先生がわざわざ記事書いてくれてるんだから、まずそれを読もう。読めば訳された記事がイマイチなのは分かると思う。
http://lyrical-logical.hatenablog.com/entry/2016/12/15/135831

“A functional language actively helps you eliminate side-effects wherever possible, and tightly control them wherever it's not.”って、住井先生の「関数型言語とは、……関数型プログラミングを推奨・支援するプログラミング言語」「（関数型プログラミングとは）副作用をできるだけ（あるいは全く）用いず、式や関数で計算を表すプログラミングスタイル」ってのとほぼ同じこと言ってますよね。まあ、住井先生の記事の方はリファレンスがちゃんと張ってあるのがいいと思います。

*1:こういう説明が簡単にできるようになるので、「副作用」と「副原因」を区別するのは有意義だと思います。

2016-10-25

プログラムを哲学する 2. 「概念記法」

プログラミング哲学

以前、言語の完全性について言及した。今回は引き続き、言語の完全性について考える。

mandel59.hateblo.jp

フレーゲの「概念記法」

フレーゲは未定義の式の存在を「言語の不完全性」（einer Unvollkommenheit der Sprache）とみなしていた。論理学者のフレーゲにとって、表現の「意味」（Bedeutung; その記号があらわしている事物。表記対象 denotation や言及対象 referent に相当すると考えられる）が確定していることは重要なことであった。表現の「意味」は、ちょうど1つでなければならず、それより多くても、少なくてもいけない。*1そのような多義的ないし無意味な表現は論理的誤謬のもととなるので、学問から排除するべきだと考えた。

フレーゲの提案した「約定」（Festsetzung）とは、そのような「言語の不完全性」を排し、言語を完全化する方法である。ある表現に「意味」が複数考えられる場合や「意味」が考えられない場合には「約定」を行うことで、あらゆる文法的に正しい表現の「意味」をただひとつに定める。簡単に言えば、「意味」がないなら（「意味」が多いなら）、「意味」を決めてやればいいというようなことだ。

数学では「√」という記号は正の平方根を表すと決めることによって、「 $\sqrt{4}$ 」が $2$ だけを表すとし、 ${-2}$ をも同時に表すことを退けているが、これも一種の「約定」だと言える。「言語の不完全性」を「約定」により避け、あらゆる表現の「意味」をただひとつに確定した「論理的に完全な言語」（einer logisch vollkommenen Sprache）をフレーゲは構想し、それを「概念記法」（Begriffsschrift）と呼んだ。フレーゲは、「言語の完全性」を達成するために、「概念記法」に次の要求を行った。

論理的に完全な言語（概念記法（Begriffsschrift））に対しては、すでに導入された記号から文法的に正しい方法によって固有名として構成された表現はすべて、実際上ある対象を表示することと、いかなる記号もそれに対する意味が保証されることなしに新たに固有名として導入されることはないという二つのことが求められている。[1]

ここで挙げられている要求は、おおむね〈構成性〉と〈原子確定性〉に相当する。（これらの用語は以前 Referential Transparencyの代わりに使える概念案 - Ryusei’s Notes (a.k.a. M59のブログ) で導入したものだ。）「概念記法」を規定する「約定」すべてに〈構成性〉と〈原子確定性〉を要求することで、「概念記法」全体の「論理的な完全性」=〈確定性〉を実現できる。*2

フレーゲの「約定」は表現の「意味」を唯一に定めることに主眼があるため、個々の「約定」に論理上の根拠は存在しない。むしろ、論理上の根拠が与えられないからこそ、約定によって表現の意味を決めるというのだろう。「約定」に論理上の根拠がなくとも、その「約定」が〈構成性〉と〈原子確定性〉を満たす形で行われるのであれば、どう「約定」しようとも「概念記法」全体の〈確定性〉は保証され、矛盾が生じることはなく、論理上は問題がない。

例えば、フレーゲは解析学の記号の「不完全性」を示す例として発散級数（収束値を持たない級数）を挙げ、発散級数はは数0を表すと「約定」することによって、この「不完全性」を排除することに言及している。この数0による「約定」はあくまでも例で、根拠があると言えないが、〈構成性〉と〈原子確定性〉を満たすどのような「約定」を行っても、矛盾が生じることはない。

出典

[1] フレーゲ, ゴットロープ (1986) 「意義と意味について Über Sinn und Bedeutung」（土屋俊訳）, 坂本百大編『現代哲学基本論文集』 1, p. 26, 勁草書房.
ドイツ語の表現はGottlob Frege. Über Sinn und Bedeutungから適宜引用

*1:フレーゲは命題文の「意味」とは真理値だと考えたから、命題文の「意味」は必ず真か偽かのどちらか一方だということでもある。

*2:追記：厳密には、原子式の意味が決定されるためには原子式の文脈が決定される必要があるため、〈文脈確定性〉も要る。

2016-05-14

文脈付き構成的意味論を構成的意味論に変換する

プログラミング哲学数学

mandel59.hateblo.jp

ここでは, 自然数の集合 ${\bf N}$ に0を含めることとする。

記法 $\left ( a_k \right )_{k=m}^{n}$ は $\left (a_m, a_{m+1}, \cdots, a_{n-2}, a_{n-1} \right )$ を表す。 $m = n$ の時は $\left ( \right )$ を表す。
記法 $\bigwedge_{k = m}^{n} p_k$ は $p_m \wedge p_{m+1} \wedge \cdots \wedge p_{n-2} \wedge p_{n-1}$ を表す。 $m = n$ の時は $\top$ （真理値の真）を表す。

形式言語

形式言語 $L = \langle F, | \bullet | \rangle$ は関手集合 $F$ , 関手の項数 $| \bullet | : F \rightarrow {\bf N}$ からなる組である。

式

形式言語 $L = \langle F, | \bullet | \rangle$ の式集合 $E(L)$ を, つぎの帰納的定義によって定める:

$f \in F \land \left ( \bigwedge_{k = 0}^{|f|} t_k \in E(L) \right ) \Rightarrow f(t_k)_{k=0}^{|f|} \in E(L)$ .

これは, 次のようなことを含意している:

が項数の関手であり, が式であるとき, は式である。
- 特に, $f$ が項数 $0$ の関手であるとき, $f()$ は式である。
$t$ が式であるとき, ある自然数 $n$ , ある項数 $n$ の関手 $f$ , ある式 $t_0, \cdots, t_{n-1}$ が存在し, $t = f(t_0, \cdots, t_{n-1})$ .

構成的意味論

構成的意味論 $\Sigma = \langle L, M, I \rangle$ は形式言語 $L = \langle F, | \bullet | \rangle$ , 意味集合 $M$ , 解釈 $I : f \in F \mapsto g \in [ M^{|f|} \rightarrow M ]$ からなる組である。

このとき $\Sigma$ のもとの式の意味 $\Sigma \unicode{x27e6} \bullet \unicode{x27e7} : E(L) \rightarrow M$ を, つぎの帰納的定義によって定める。

$\Sigma \unicode{x27e6} f(t_k)_{k=0}^{|f|} \unicode{x27e7} = I(f) \left ( \langle \Sigma \unicode{x27e6} t_k \unicode{x27e7} \rangle_{k=0}^{|f|} \right )$

文脈付き構成的意味論

文脈付き構成的意味論 $\Sigma_\star = \langle L, C, V, I_\star \rangle$ は形式言語 $L = \langle F, | \bullet | \rangle$ , 文脈集合 $C$ , 値集合 $V$ , 解釈 $I_\star : f \in F \mapsto g \in [ [ C \rightarrow V ]^{|f|} \rightarrow [ C \rightarrow V ] ]$ からなる組である。

このとき $\Sigma_\star$ のもとの式の意味 $\Sigma_\star \unicode{x27e6} \bullet \unicode{x27e7} : E(L) \rightarrow [ C \rightarrow V ] \$ を, つぎの帰納的定義によって定める。

$\Sigma_\star \unicode{x27e6} f(t_k)_{k=0}^{|f|} \unicode{x27e7} = I_\star(f) \left ( \langle \Sigma_\star \unicode{x27e6} t_k \unicode{x27e7} \rangle_{k=0}^{|f|} \right )$

文脈 $c \in C$ のもとの式 $e$ の値は $\Sigma_\star \unicode{x27e6} e \unicode{x27e7} (c) \$ になる。

文脈付き構成的意味論を構成的意味論に変換する

文脈付き構成的意味論 $\Sigma_\star = \langle L, C, V, I_\star\rangle$ から自明な構成的意味論 $\Sigma ' _\star = \langle L, [ C \rightarrow V ], I_\star \rangle$ を構成できる。

2016-05-11

プログラム意味論の分かりやすい紹介

プログラミング哲学

巷に膾炙しているプログラム意味論の説明は、正直言って何を言っているのか、部外者にはよく分からないように感じられる。プログラムの意味を論じる「プログラム意味論」の意味がよくわからないというのは本末転倒だろう。ここでは、プログラム意味論を分かりやすく紹介したい。

プログラムの意味

プログラム意味論とは、プログラムの意味に関する理論だ。

そもそも「意味」とはなんだろうか。「意味」の意味を知るために、デジタル大辞泉で調べてみよう。

１言葉が示す内容。また、言葉がある物事を示すこと。「単語の―を調べる」「愛を―するギリシャ語」
２ある表現・行為によって示され、あるいはそこに含み隠されている内容。また、表現・行為がある内容を示すこと。「慰労の―で一席設ける」「―ありげな行動」「沈黙は賛成を―する」
３価値。重要性。「―のある集会」「全員が参加しなければ―がない」
いみ【意味】の意味 - goo国語辞書

「意味」の語義が3つ示されているが、要約すると、ひとつめは「言葉が示す物事」、ふたつめは「行為が示す物事」、みっつめは「行為が持つ価値」だ。この3つの「意味」の意味は無関係なものではなく、共通した構造が存在している。それは、何か言葉や行為という表に見えている表現は、その裏にある物事や価値に繋がっているという構造だ。

たとえば、店で「ビールあり〼」という看板を見たとする。ビールの実物を見ずとも、その店には実際にビールが用意されていて、店はそのビールを売る意図があって、自分はそれを注文して飲むことができるという場面を想像できる。その想像された場面や、その場面の持っている価値が、「ビールあり〼」の意味だと言える。

プログラムの意味も同様だ。プログラムの意味とは、そのプログラムによって実現される物事や場面のことだと言える*1。例えばalert(1)というJavaScriptのプログラムは、実行するとダイアログ・ボックスで“1”を表示する。すなわち、alert(1)の意味は「ダイアログ・ボックスで“1”を表示する」という場面だ。

プログラムの意味は、そのプログラムを動かしてみれば分かるように思うかもしれないが、プログラムを動かすにもコストやリスクが存在する場合がある。誤作動を起こすプログラムを実際に動かしてしまえば、重大な事故を引き起こすかもしれない。それを避けるためには、プログラムを動かすことなく、その意味を知る必要があるのだ。

優れたプログラマーが頭の中で考えたプログラムを一発で動かしてしまうのも、プログラムの意味を体得しているからだと言える。しかし、プログラムの意味を個人の経験によって身に付けるのは時間がかかるだけではなく、その厳密さにも限界がある。見慣れない種類のプログラムがどのように動くかは、経験からでは分からないのだ。そういう場合でも、プログラム意味論でプログラムの表現と物事の間にある関係を詳細に学ぶことで、プログラムの意味を正確に把握できるようになるだろう。

形式的意味論

意味論は表現と物事の対応を論じるものではあるけれど、現実の物事はすごく複雑で、それをありのままに考えて厳密に論じるのはとても難しい。そこで、普通は物事を抽象化した上で、厳密に考えることになる。*2物事を抽象化した上で、数学や論理学を使って厳密に論じられる意味論が、形式的意味論だ。形式的意味論には操作的意味論、表示的意味論、公理的意味論といった大別がある。

操作的意味論は、表現を操作する規則や抽象機械を使ってプログラムの意味を考える。この意味論では表現の操作過程や抽象機械の動作が、表現の意味となる。この意味論は、現実のコンピューターの動作に一番近い形で表現された意味論で、プログラムに対して、機械がどれほどの計算資源を使い、どのように動作するのかを厳密に議論するのに適した表現だと言える。その一方で、操作的意味論が扱った規則以外の方法でプログラムを処理することについては考慮しないので、プログラムの読みやすさや編集しやすさを議論するには適していないだろう。

表示的意味論は、表現から物事への写像（表示）を使ってプログラムの意味を考える。この意味論においては、表現からの写像が定義できる好きな領域を意味としてよい。この手法は、言語の意味を数理論理学や言語哲学と同様の手法を用いて考えており、プログラムを読み書き・編集するときの性質を分析するのに向いている。例えばプログラミング言語が「構成性」という性質を持っていることが意味論から分かるので、その性質を利用したプログラムの最適化を行う、といったことに使える。

公理的意味論は、表現と物事の間に成り立つ関係（仕様）を使ってプログラムの意味を考える。この意味論においては、仕様を公理として証明できる物事が、表現の意味となる。この意味論では、仕様にないプログラムの具体的な動き方は分からないが、プログラムの「停止性」のような抽象度のより高い性質を証明するのに向いている。

リファレンス

【PDF】 Computer Science 203 Programming Languages Axiomatic Semantics

*1:「実行結果」と言ってしまえば済むように思うが、サーバーのように継続的に実行され続けるプログラムや、ギャンブル・ゲームのように非決定的な振る舞いをするプログラムもあるわけで、そのようなプログラムの意味も考えようとすると、単に「実行結果」と言うだけでは済まない。

*2:ここで「厳密に論じる」と言っているのは、他人に自分の論理を説明できる形で、論理的に論じるということだ。論じる問題が複雑になると、関係しあう事柄の組み合わせが爆発的に増えるせいで、論理を構成するのが極端に難しくなってしまう。だから、抽象化を行うことで一度に考える事柄を減らし、問題を厳密に論じきれる大きさにする必要がある。

2016-05-05

プログラミングと哲学

哲学プログラミング

プログラミングと哲学の間には深い関係がある。プログラミングが昔ながらの哲学と単純に対応するというわけではないけれども、だからといって全くの無関係というわけでもない。その理由として、プログラミングの方法論のひとつに、世界を分析し、それを記述するという方法でプログラムを書くという考えがあることが挙げられる。

それはまさにオブジェクト指向の理念である、と考える人は、プログラミングのことも哲学のこともよく知らない。世界の様子を記述するという性質はオブジェクト指向の専売特許などではなく、平叙型プログラミング*1に共通して見られる考えだ。すなわち、関数型プログラミングや論理型プログラミングもまた、世界の様子を記述する側面を持っている。

「世界を分析して記述する方法」というのは、古来哲学が対象としてきたことのひとつだ。それなら、哲学なんてプログラミングと関係ないとするほうが、伝統に則らない考えだというべきだろう。分かりやすい例として、論理型プログラミングと分析哲学の関係を挙げる。論理型プログラミングの記法は記号論理学に由来するが、遡ればフレーゲの「概念記法」にたどり着く。フレーゲは一方で分析哲学の祖ともされるが、フレーゲの分析哲学とは、概念記法の背景にある考えを記述したものに他ならない。

あなたが論理学や論理型プログラミング言語を使っている時、あなたはその背景にある「世界の分析方法」をも、気づかないうちに体得している。そういう無意識のうちに使っている考え方を、哲学者は積極的に言語化してくれているのだ。分析哲学を知らなくても論理学を使えるかもしれないが、分析哲学を知ることで論理学自体をよりよく知ることができる。

プログラミングと哲学を結びつけて考えるというのは、古臭い考えを無批判に受け入れるということでもなければ、突飛なこじつけをするというものでもない。むしろその反対だ。自分が無意識に使っている概念があることを既存の哲学を通して自覚することで、プログラミングをより深く理解し、批判的に接することができるようにする。古い哲学が自分の考え方を完全に説明していると思われなければ、新しく考えを付け足していく。そういう営みを意識的に行うことが、プログラミングと哲学を結びつけて考える意義だろうと思う。

*1:declarative programming. 定訳は「宣言型プログラミング」だが、言語学では「命令文 imperative sentence」「平叙文 declarative sentence」と言うのだから、当然「命令型プログラミング imperative programming」に対して「平叙型プログラミング」と訳すべきだ。

2016-04-06

Referential Transparencyの代わりに使える概念案

プログラミング哲学

Referential Transparencyという概念が指すものは漠然としているので、もっと意味が明瞭で使いやすい用語を定義し、色々な言語の性質を記述してみる。

前提として

式は原子式か複合式である。
複合式は関手（functor）と項（argument）から構成される。

〈純粋性〉: 「式の意味」と「式の値」は同義である。
〈原子確定性〉: 原子式の意味は原子式自身とその原子式の文脈から決定される。
〈構成性〉: 複合式の意味は関手および項の意味から決定される。
〈弱構成性〉: 複合式の意味は関手、項の意味および式の文脈から決定される。
〈文脈構成性〉: 複合式の項の文脈は、その複合式の文脈と関手から決定される。
〈文脈弱構成性〉: 複合式の項の文脈は、その複合式の文脈、関手および他の項の意味から決定される。
〈確定性〉: 式と式の文脈から部分式の意味が決定される。
〈文脈確定性〉: 式と式の文脈から部分式の文脈が決定される。
〈文脈同一性〉: 部分式は式全体と同じ文脈を持つ。
〈同値置換可能性〉: 部分式を、その式と同値の別の部分式に置き換えても、式全体は同じ意味を持つ。

関手がすべて全関数である数式は〈原子確定性〉〈構成性〉〈文脈同一性〉を持つので、〈確定性〉がある。たとえば、 $\{ a \mapsto 2, b \mapsto 3 \}$ という文脈において、式 $a + b$ は確定した値 $5$ を持つ。また、同じ変数は、ひとつの式の中では常に同じ値を指す。
C言語においては普通「式の値」でなく、副作用を含めた「式の動作」が「式の意味」だと考えるので、C言語は〈純粋性〉を持たないと言える。
Haskellにおいては普通「式の値」が「式の意味」だと考えるので、Haskellは〈純粋性〉を持つと言える。
関手がすべて全関数である数式に非再帰的なlet式を加えても〈原子確定性〉〈弱構成性〉〈文脈弱構成性〉〈確定性〉は保たれる。

（〈弱構成性〉は、レカナティの「語用論的構成性」と同様の概念か。 http://www.wakate-forum.org/data/tankyu/42/42_09_takaya.pdf）

2016-04-01

Referential Transparencyについて取り急ぎ

プログラミング哲学

Wikipedia日本語版に

参照透過性（さんしょうとうかせい、英: Referential transparency）は、計算機言語の概念の一種で、文脈によらず式の値はその構成要素（例えば変数や関数）によってのみ定まるということを言う。
https://ja.wikipedia.org/w/index.php?title=%E5%8F%82%E7%85%A7%E9%80%8F%E9%81%8E%E6%80%A7&oldid=46720534

とあるが、これは誤り。「文脈によらず式の値はその構成要素によってのみ定まる」という性質は、参照透過性ではなく構成性 (compositionality) と言う。

In mathematics, semantics, and philosophy of language, the principle of compositionality is the principle that the meaning of a complex expression is determined by the meanings of its constituent expressions and the rules used to combine them.
https://en.wikipedia.org/w/index.php?title=Principle_of_compositionality&oldid=646872914

The meaning of a complex expression is determined by its structure and the meanings of its constituents.
http://plato.stanford.edu/entries/compositionality/

参照透過性は、英語版 Wikipediaによれば次の性質だ。

An expression is said to be referentially transparent if it can be replaced with its value without changing the behavior of a program (in other words, yielding a program that has the same effects and output on the same input).
ある式は、その式をその式の値に置き換えてもプログラムの動作が変わらないとき（いいかえれば、同じ入力に対して同じ作用と出力を持つプログラムになるとき）、参照透過であるという。
https://en.wikipedia.org/w/index.php?title=Referential_transparency&oldid=709215227

（この定義が正しいとは限らないが、日本語版の説明と食い違っていることは明らかだ。）

問題をややこしくするのは、式 (expression)、意味 (meaning) 、表現 (representation)、正規形 (regular form)、表示 (denotation)、参照 (reference)、値 (value)、動作 (behavior) といった用語が、文脈によってそれぞれ同義になったりならなかったりして、混同されるというところだ。それについては別に整理してまとめることにする。

2016-03-01

プログラミングにおける〈式〉の考察まとめ

index プログラミング哲学

mandel59.hateblo.jp
mandel59.hateblo.jp